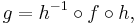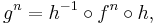Topological conjugacy

In mathematics, two functions are said to be topologically conjugate to one another if there exists a homeomorphism that will conjugate the one into the other. Topological conjugacy is important in the study of iterated functions and more generally dynamical systems, since, if the dynamics of one iterated function can be solved, then those for any topologically conjugate function follow trivially.

To illustrate this directly: suppose that f and g are iterated functions, and there exists an h such that

$g=h^{-1}\circ f\circ h,$

so that f and g are topologically conjugate. Then of course one must have

$g^n=h^{-1}\circ f^n\circ h,$

and so the iterated systems are conjugate as well. Here, 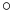$\circ$ denotes function composition.

1 Definition
2 Examples
3 Discussion
4 Topological equivalence
5 Generalizations of dynamic topological conjugacy
6 Cited References
7 See also

Definition

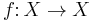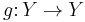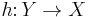Let $X$ and $Y$ be topological spaces, and let $f\colon X\to X$ and $g\colon Y\to Y$ be continuous functions. We say that $f$ is topologically semiconjugate to $g$ , if there exists a continuous surjection $h\colon Y\to X$ such that 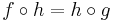$f\circ h=h\circ g$ . If $h$ is a homeomorphism, then we say that $f$ and $g$ are topologically conjugate, and we call $h$ a topological conjugation between $f$ and $g$ .

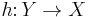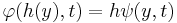Similarly, a flow $\varphi$ on $X$ is topologically semiconjugate to a flow $\psi$ on $Y$ if there is a continuous surjection $h\colon Y\to X$ such that $\varphi(h(y),t) = h\psi(y,t)$ for each 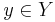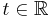$y\in Y$ , $t\in \mathbb{R}$ . If $h$ is a homeomorphism then $\psi$ and $\varphi$ are topologically conjugate.

Examples

the logistic map and the tent map are topologically conjugate. ^[1]
the logistic map of unit height and the Bernoulli map are topologically conjugate.

Discussion

Topological conjugation defines an equivalence relation in the space of all continuous surjections of a topological space to itself, by declaring $f$ and $g$ to be related if they are topologically conjugate. This equivalence relation is very useful in the theory of dynamical systems, since each class contains all functions which share the same dynamics from the topological viewpoint. For example, orbits of $g$ are mapped to homeomorphic orbits of $f$ through the conjugation. 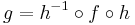Writing $g = h^{-1}\circ f\circ h$ makes this fact evident: 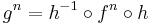$g^n = h^{-1}\circ f^n \circ h$ . Speaking informally, topological conjugation is a “change of coordinates” in the topological sense.

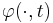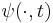However, the analogous definition for flows is somewhat restrictive. In fact, we are requiring the maps $\varphi(\cdot,t)$ and $\psi(\cdot,t)$ to be topologically conjugate for each $t$ , which is requiring more than simply that orbits of $\varphi$ be mapped to orbits of $\psi$ homeomorphically. This motivates the definition of topological equivalence, which also partitions the set of all flows in $X$ into classes of flows sharing the same dynamics, again from the topological viewpoint.

Topological equivalence

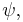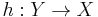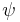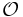We say that $\psi,$ and $\varphi$ are topologically equivalent, if there is a homeomorphism $h:Y\to X$ , mapping orbits of $\psi\,$ to orbits of $\varphi$ homeomorphically, and preserving orientation of the orbits. In other words, letting $\mathcal{O}$ denote an orbit, one has

$h(\mathcal{O}(y,\psi)) = \{h(\psi(y,t)): t\in\mathbb{R}\} = \{\varphi(h(y),t):t\in\mathbb{R}\}= \mathcal{O}(h(y),\varphi)$

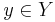for each $y\in Y$ . In addition, one must line up the flow of time: for each 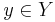$y\in Y$ , there exists a 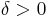$\delta>0$ such that, if 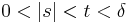$0<\vert s\vert< t < \delta$ , and if $s$ is such that $\varphi(h(y),s) = h(\psi(y,t))$ , then $s>0$ .

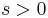Overall, topological equivalence is a weaker equivalence criterion than topological conjugacy, as it does not require that the time term is mapped along with the orbits and their orientation. An example of a topologically equivalent but not topologically conjugate system would be the non-hyperbolic class of two dimensional systems of differential equations that have closed orbits. While the orbits can be transformed each other to overlap in the spatial sense, the periods of such systems cannot be analogously matched, thus failing to satisfy the topological conjugacy criterion while satisfying the topological equivalence criterion.

Generalizations of dynamic topological conjugacy

There are two reported extensions of the concept of dynamic topological conjugacy:

1. Analogous systems defined as isomorphic dynamical systems

2. Adjoint dynamical systems defined via adjoint functors and natural equivalences in categorical dynamics^[2]^[3].

Cited References

^ Alligood, K. T., Sauer, T., and Yorke, J.A. (1997). Chaos: An Introduction to Dynamical Systems. Springer. pp. 114–124. ISBN 0387946772.
^ http://planetphysics.org/encyclopedia/Complexity.html Complexity and Categorical Dynamics
^ http://planetphysics.org/encyclopedia/AnalogousSystems3.html Analogous systems, Topological Conjugacy and Adjoint Systems